An oscillatory network model of Head direction and Grid cells using locomotor inputs
We present a model of head direction (HD) and grid cells formed purely from idiothetic (locomotor) inputs. Grid cells are a class of spatial cells located in the medial Entorhinal Cortex which is assumed to perform path integration and characterized by its unique hexagonal firing fields. Empirically it is proven that HD cells, another class of spatial cells which encode the heading direction of an animal, form the major input to the grid cell. Existing computational models of grid cells make artificial assumptions like existence of HD cells with a phase differences that are integral multiples of 60 degrees. The aim of the study is to model grid cell firing without imposing these special constraints
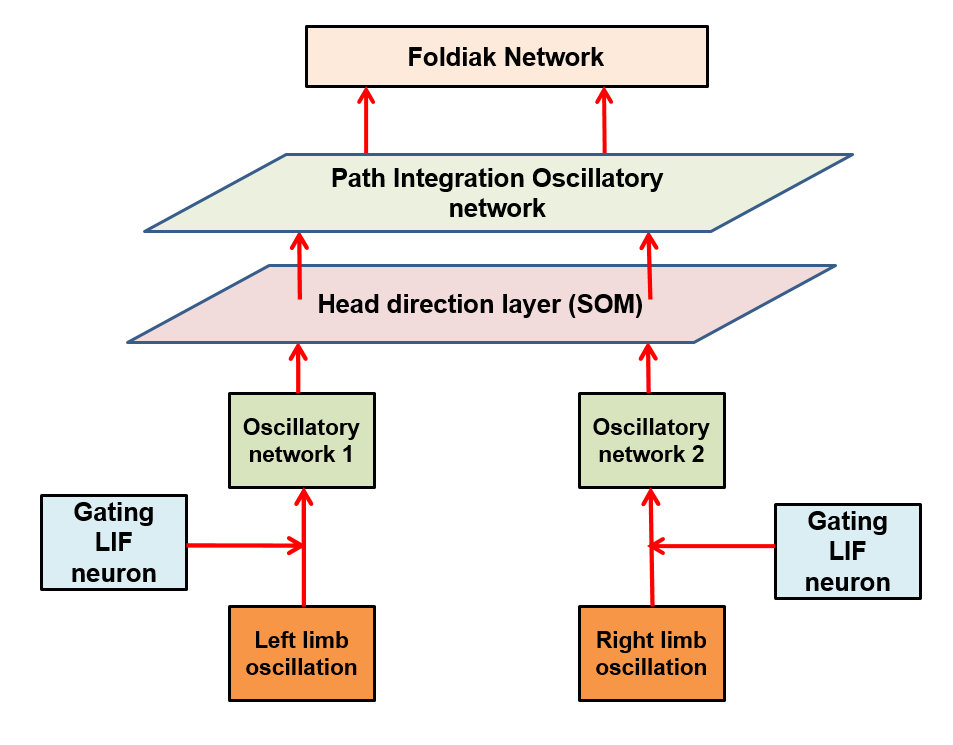
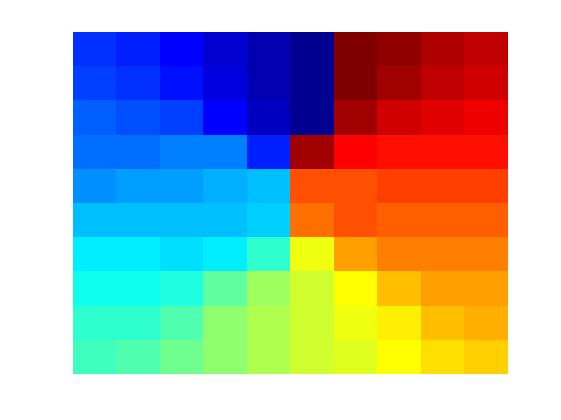
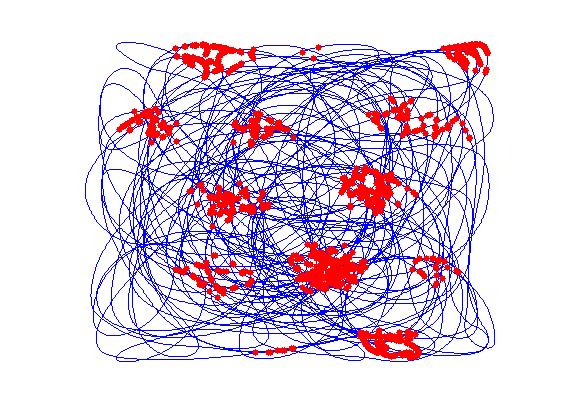
The model (Figure a) takes proprioceptive inputs coming from the joint angles of the two limbs. Locomotor rhythms are modeled as two sinusoidal oscillators whose amplitudes are modulated by the curvature and the speed of simulated animal. These inputs are gated using a Leaky Integrate and Fire (LIF) neuron that spikes at a fixed frequency so that the curvature and speed information from respective limb oscillations are extracted out and given to two oscillatory neural networks separately. The oscillatory neural networks are modeled as Kuramoto networks in which the phase is modulated by the curvature of the path traversed by the simulated animal. Synchrony between the two clusters of oscillators is quantified in terms of sine and cosine of phase difference between the two pools of oscillators. The synchrony parameters are further used to train a one dimensional Self Organizing Map (SOM), whose neurons display head direction-tuned responses (Figure b). Each HD response is further given to a path integration (PI) layer. PI layer is again a network of Kuramoto oscillators whose phase is integrated as a function of HD responses. PI values were further given as input to Foldiak network. After training, weights of the Foldiak network converged to the subspace of the PC’s of the input vectors. While remapping the neural response of the Foldiak hexagonal grid fields, square grid fields, border cells were observed (Figure c). Hence this is a generalized model which provides a theoretical basis for the formation of both hexagonal and non hexagonal grid fields and possibly other spatial cells which are actually projections of the PI values onto its PCA subspace.
Karthik Soman, Vignesh Muralidharan and V. S. Chakravarthy, "An oscillatory network model of Head direction and Grid cells using locomotor inputs," CNS, Jeju Island, South Korea, 2016 (Abstract Accepted).
A Computational model of Hippocampus inspired by the functional architecture of Basal Ganglia
We present a networkmodel of hippocampus (HC) inspired by the functional architecture of the basal ganglia (BG). The model describes the role of hippocampus in spatial navigation and is cast in Reinforcement Learning (RL) framework (Figure a). There is a corpus of literature which states that hippocampus is a key player in spatial learning because of the enriched sensory information that arrives at the portals of HC, the entorhinal cortex (EC), from the sensory cortical areas. The model simulates the Morris water maze task wherein a virtual agent navigates inside a circular pool to find an invisible platform using the spatial context from the environment.
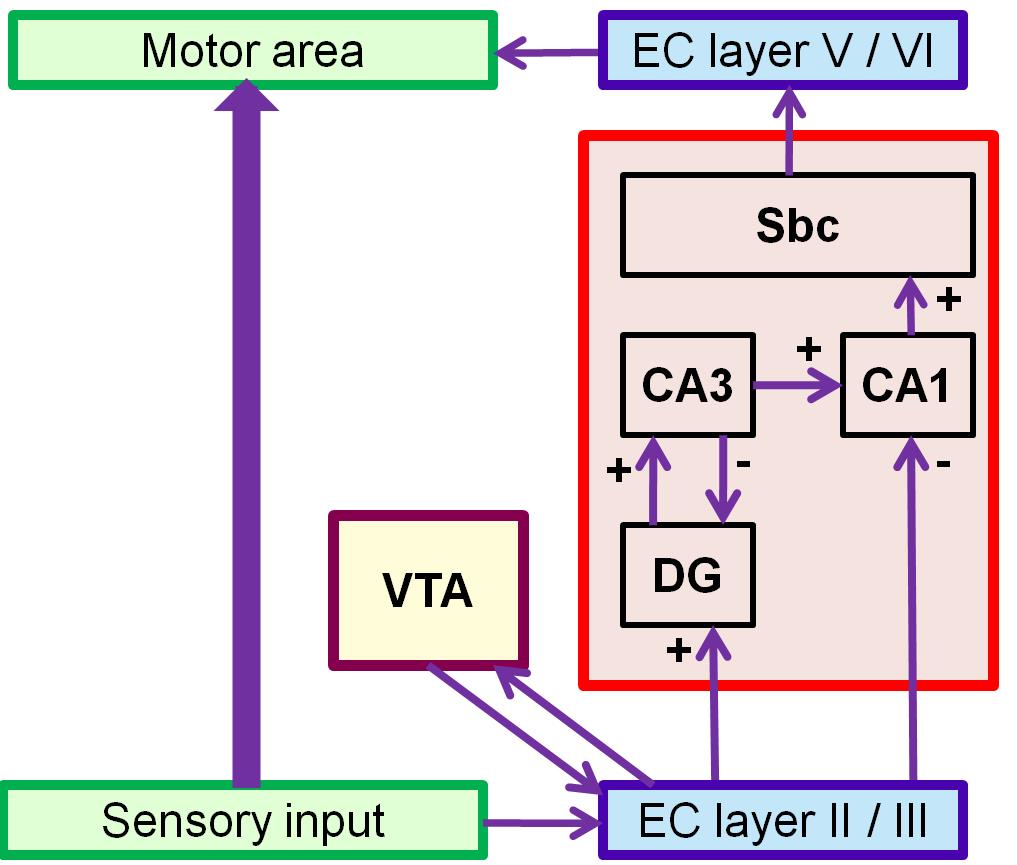
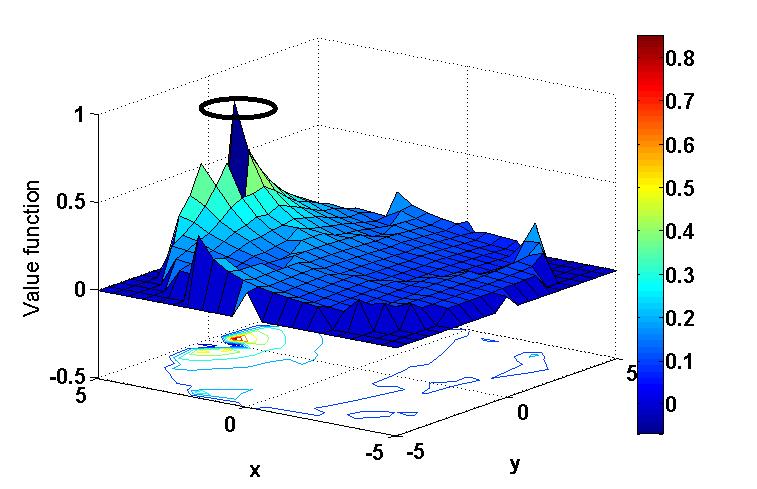
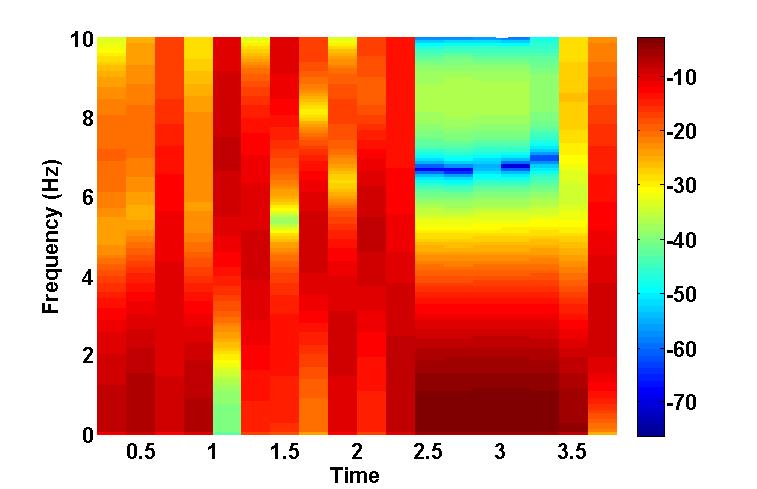
In order to model the ability of HC to learn spatial context, we simulate a circular pool surrounded by six distinguishable poles of equal heights. As the agent/animal navigates, the size of retinal image of each pole varies with distance between the agent and the pole. Reward is given to the agent when it reaches the platform. The abstract form of the visual input is given to EC which has afferent and efferent projections from Ventral Tegmental Area (VTA), one of the dopamine centers in the mid brain. Temporal Difference (TD) error generated from VTA is used to update the synaptic weights for Value computation of the sensory input in EC. Additionally an action vector defining the direction of the agent’s next step also forms a feedback input to the EC. We describe the functional anatomy of HC in terms of two pathways: a direct pathway between EC and CA1 and an indirect pathway between EC and CA1 via Dentate Gyrus (DG), and CA3. A quantity known as Value difference, that represents afferent dopamine signals in EC, is thought to control switching between these pathways. Desynchronized activity generated by the DG –CA3 loop in the indirect pathway aids the agent to explore the space. Direct pathway facilitates the agent’s navigation. The difference in the responses from these two pathways is computed in CA1 and is relayed to subiculum (Sbc) which computes the direction of the next step. Output of SBc is communicated to higher motor areas (MC), modeled as a 1-D Continuous attractor neural network, via deeper layers of EC. MC also receives direct inputs from sensory areas so that the output of MC is the weighted sum of responses from the sensory cortical areas and HC respectively. MC response is used to update the next step. Cortico-cortical connections are updated using the TD error as well as the velocity generated from HC as a target. As the value function matures (Figure b), contribution from HC declines; the acortico-cortical connections gain the upper hand and the agent reaches the platform faster. Thus, after training, Cortico-cortical pathway (CCP) can drive navigation without the involvement of HC. Analysis of CA3 activity shows desynchronization during active exploration and synchronizationupon reaching the platform (Figure c). This resonates with experimental results suggesting that low-amplitude theta waves correspond to desynchronized activity during exploration, whereas the sharp waves during non-exploratory states correspond to synchronized activity .
Karthik Soman, Vignesh Muralidharan and V. S. Chakravarthy, "A Computational model of Hippocampus inspired by the functional architecture of Basal Ganglia," CNS, Jeju Island, South Korea, 2016 (Abstract Accepted).